堆排序的平均性能是O(n*logn),虽然对于不同的数据性能并不稳定,但由于需要的辅助空间很小,所以是一个很常用的排序算法。
堆排序的基本原理是利用大(小)顶堆的特性,对于一个二叉树中的节点,假设所有节点的左右孩子节点值都不大(小)于父亲节点,那么这个二叉树就叫做大(小)顶堆。
对于一个大(小)顶堆,位于根节点的值一定是最大(小)的,所以堆排序的过程就是创建、调整大(小)顶堆的过程。
下面以大顶堆排序为例说明,有一个整型数组:
324 93 921 122 308 434 705 373 145 608 239 758
根据数组创建一棵二叉树:
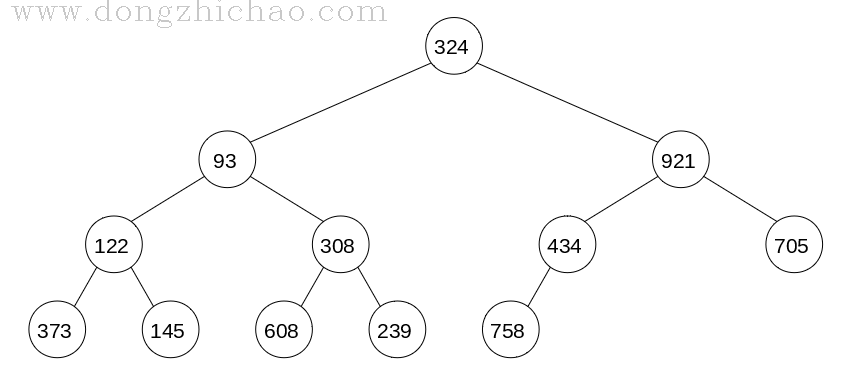
原则是:
(1) 根节点对应数组下标为0的数据;
(2) 当前节点下标为N,则左孩子节点的下标为2*N+1;
(3) 当前节点下标为N,则右孩子节点的下标为2*N+2;
由于叶子结点没有孩子节点,我们可以将叶子节点看做已经创建好的大顶堆,所以创建大顶堆就从最后一个非叶子结点开始,调整的算法为:
step 1: 父亲节点与左右孩子节点中最大的节点进行交换;
step 2: 如果交换后的孩子节点并非叶子结点而且不是大顶堆,则重复步骤step 1;
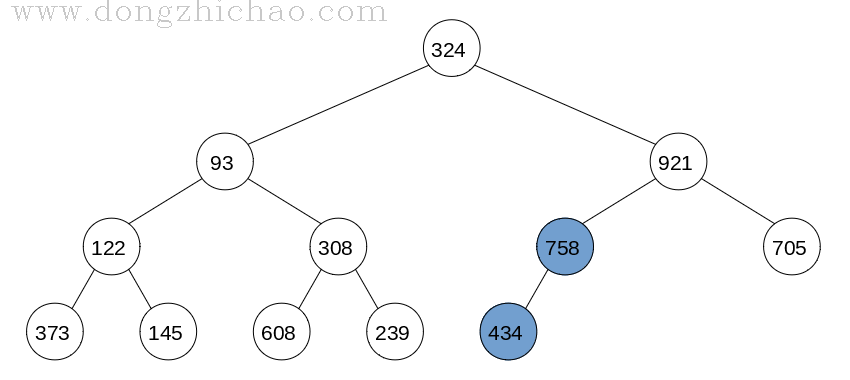
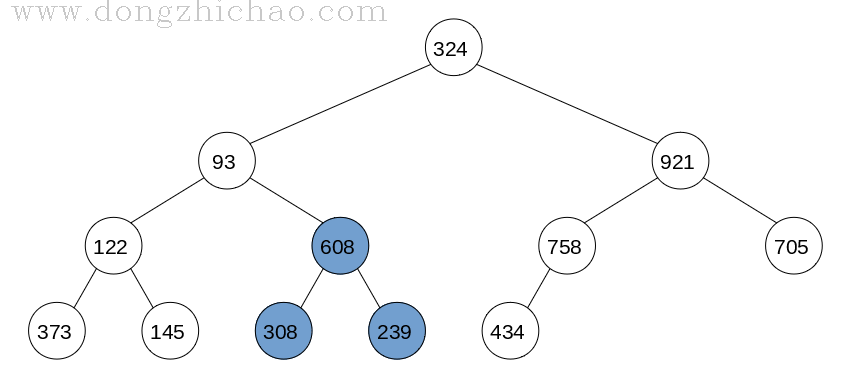
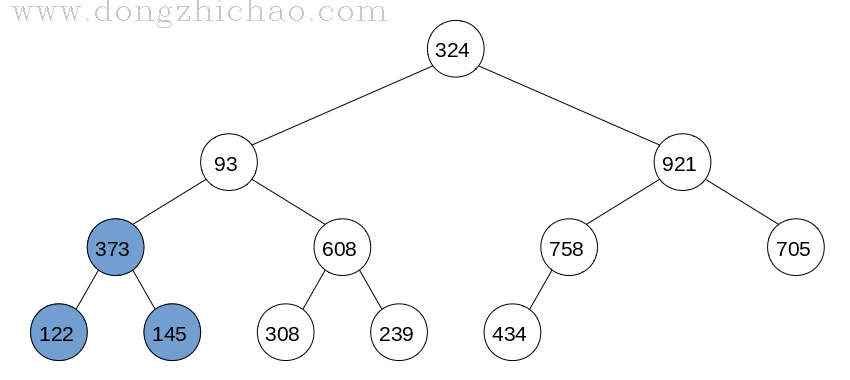
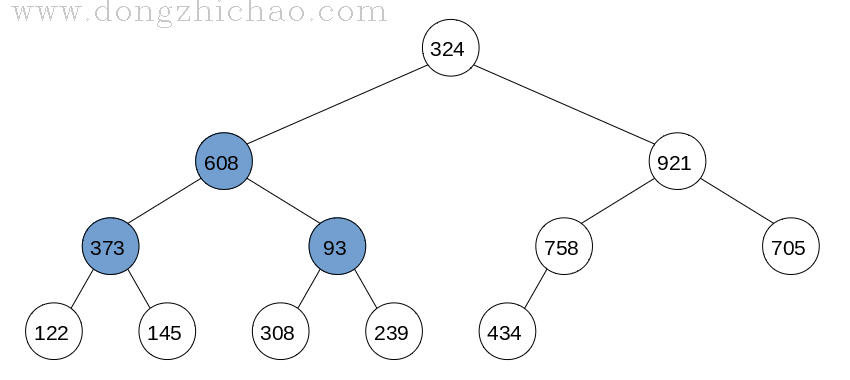
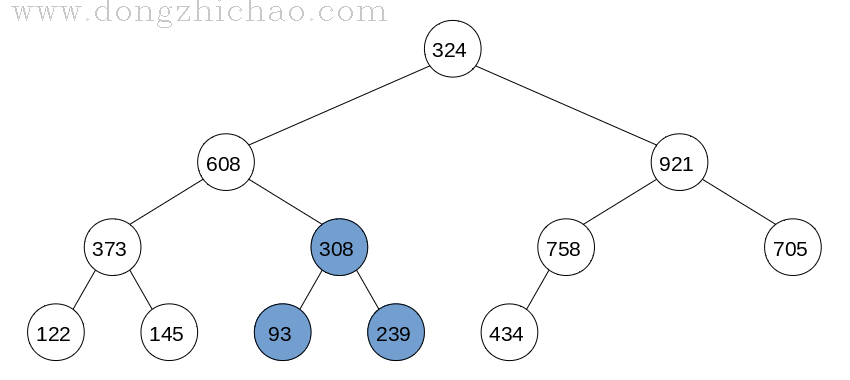
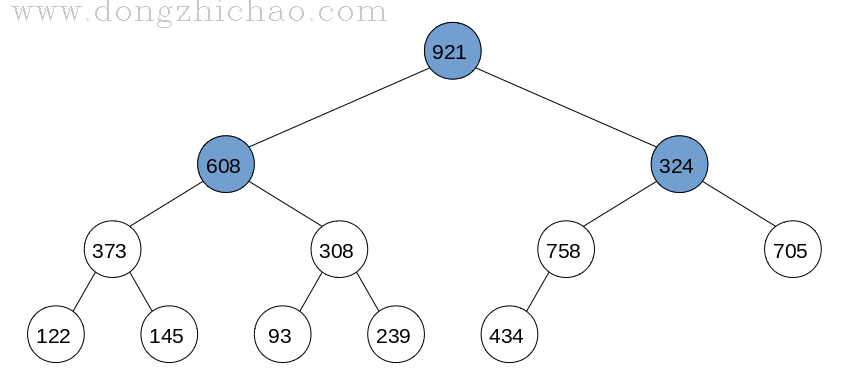
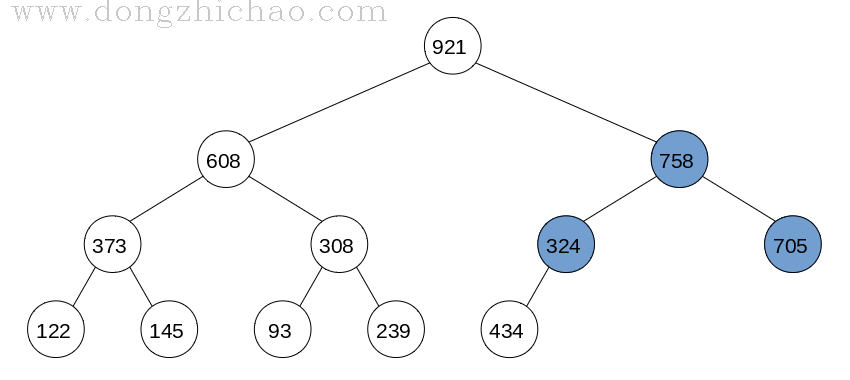
最终完成的大顶堆如下图所示:
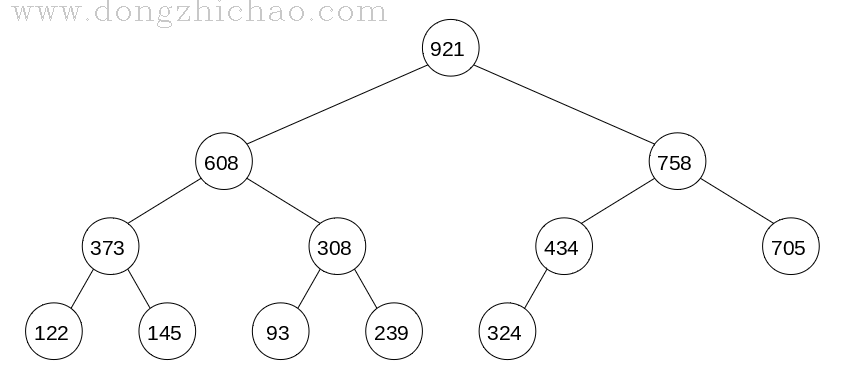
数组中数据为:921 608 758 373 308 434 705 122 145 93 239 324
而之后排序的过程就是从大顶堆根节点取数据的过程,
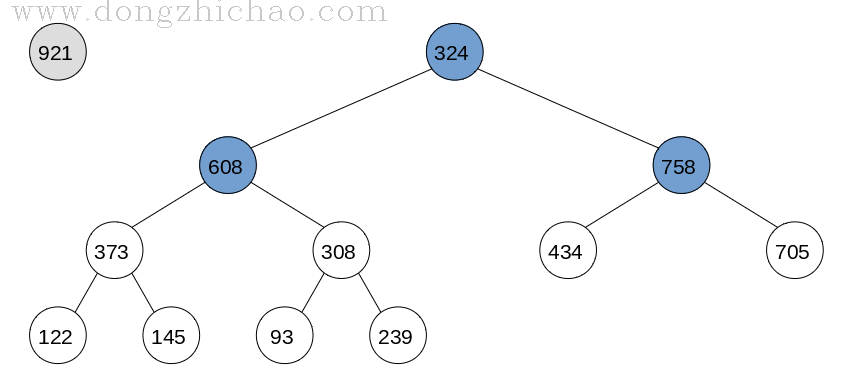
具体算法如下:
Step 1: 将根节点与最后一个叶子结点交换,并且将大堆节点个数减1;
Step 2: 从新的根结点开始重新调整堆为大顶堆;
Step 3: 从Step 1重新开始,直到堆中节点个数为2;
Step 4: 交换最后两个节点中的值;
C代码实现如下:
/* 创建大顶堆 */ int _create_max_heap(int* in, int len) { int t_node; if(len%2 == 0) t_node = (len-1)/2; else t_node = (len-2)/2; while(t_node >= 0){ _re_adjust_heap(in, t_node, len); t_node--; } return 0; } /* 调整大顶堆 */ int _re_adjust_heap(int* in, int pos, int len) { if(len <= 2) return -1; while(pos < len){ int left, right; left = pos*2+1; right= pos*2+2; if(left >= len) break; if(right >= len && in[pos]<in[left]){ _exchange_with_left(in, pos, len); break; } if(in[pos] > in[left] && in[pos] > in[right]) break; if(in[left] > in[pos] && in[left] > in[right]){ _exchange_with_left(in, pos, len); pos = left; continue; } if(in[right] > in[pos] && in[right] > in[left]){ _exchange_with_right(in, pos, len); pos = right; continue; } } } |
完整代码可以我已经push到github中,请访问:https://github.com/plumpyomi/algorithm.git