算法导论——AVL Tree

山河技术, 程序算法, 软件开发
最近由于事情太多，导致好几天没有学习新的东西，心里不禁产生一丝负罪感。
前几天看新闻说美国入境已经开始考察平衡树算法了，吓得我赶紧拿起算法导论压压惊。
遥想十几年前我还是一个本科生的时候，就被各种二叉树、二叉搜索树、B+树、B-树、红黑树烧死了无数脑细胞，今日复习看来依然心有余悸。
AVT Tree是从二叉搜索树演化而来的。
二叉搜索树是一类特殊的二叉树，其特点是：
左孩子永远比根节点小，右孩子永远比根节点大。
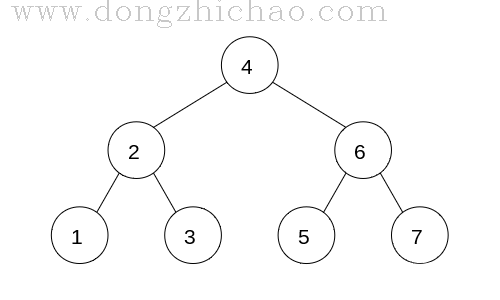
avl_tree_01
由于这个特性，二叉搜索树中的任意节点，左子树中的所有节点都比该节点小，右子树中所有的节点都比该节点大，所以搜索的时间复杂度平均可以达到O(log(n))。
但二叉搜索树会出现一个最坏的情况，
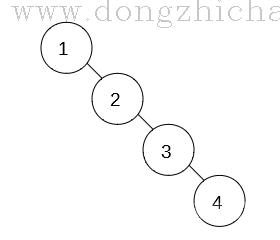
avl_tree_02
当所有节点拍成了一条直线，时间复杂度就下降到O(n)。
于是有了，AVL Tree，其特点是：任意节点的左右两颗子树高度之差的绝对值不超过1，这叫做树的平衡。
当新增或删除节点后，破坏了平衡，就需要进行旋转。
一共有八种情况，四种方法进行旋转，网上大把有的说明，这里就不多说了，直接上算法吧。
（注：旋转算法说明，可以参考http://blog.csdn.net/collonn/article/details/20128205）
（1） 定义AVL Tree节点结构
1
2
3
4
5
6

typedef struct avl_tree_node{
	int		val;
	int		depth;		//节点深度，叶子结点深度为1
	struct avl_tree_node* p_left;
	struct avl_tree_node* p_right;
} avl_tree_node_t;
（2） 插入新节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

avl_tree_node_t* __avl_tree_insert(avl_tree_node_t *p_node, int val)
{
	if(p_node == NULL){/* 新增叶子结点 */
		p_node = (avl_tree_node_t*)malloc(sizeof(avl_tree_node_t));
		if(p_node == NULL)
			return NULL;
		p_node->val		= val;
		p_node->depth	= 1;
		p_node->p_left	= NULL;
		p_node->p_right	= NULL;
	}else{
		int l_depth, r_depth;
		rotate_type_t t_type;
 
		if(val < p_node->val){
			p_node->p_left = __avl_tree_insert(p_node->p_left, val);
		}else{
			p_node->p_right = __avl_tree_insert(p_node->p_right, val);
		}
		/* 获取做右子树高度 */
		__get_avl_lr_depth(p_node, &l_depth, &r_depth);
		/*  当前结点高度=MAX(左子树高度，右子树高度) +1 */
		p_node->depth = ((l_depth>r_depth)?l_depth:r_depth)+1;
 
		/* 检查是否需要旋转 */
		t_type = __check_avl_tree_rotate(p_node, l_depth, r_depth);
		if(t_type != UNDEFINED){
			p_node = __avl_tree_rotate(p_node, t_type);
		}
	}
 
	return p_node;
}
（3） 定义四种旋转方式
1
2
3
4
5
6
7

typedef enum {
	UNDEFINED,
	L_ROTATE,	/* 左旋 */
	R_ROTATE,	/* 右旋 */
	R_L_ROTATE,	/* 先右旋后左旋 */
	L_R_ROTATE	/* 先左旋后右旋 */
} rotate_type_t;
（4） 根据做右子树高度判旋转方式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

rotate_type_t __check_avl_tree_rotate(avl_tree_node_t *p_node, int l_depth, int r_depth)
{
	int t_ld, t_rd;
 
	if(l_depth == 2 && r_depth == 0){
		__get_avl_lr_depth(p_node->p_left, &t_ld, &t_rd);
		if(t_ld == 1 && t_rd == 0)
			return L_ROTATE;
		if(t_ld == 0 && t_rd == 1)
			return R_L_ROTATE;
	}
	if(l_depth == 0 && r_depth == 2){
		__get_avl_lr_depth(p_node->p_right, &t_ld, &t_rd);
		if(t_ld == 0 && t_rd == 1)
			return R_ROTATE;
		if(t_ld == 1 && t_rd == 0)
			return L_R_ROTATE;
	}
	if(l_depth == 3 && r_depth == 1){
		__get_avl_lr_depth(p_node->p_left, &t_ld, &t_rd);
		if(t_ld == 2 && t_rd == 1)
			return L_ROTATE;
		if(t_ld == 1 && t_rd == 2)
			return R_L_ROTATE;
	}
	if(l_depth == 1 && r_depth == 3){
		__get_avl_lr_depth(p_node->p_right, &t_ld, &t_rd);
		if(t_ld == 1 && t_rd == 2)
			return R_ROTATE;
		if(t_ld == 2 && t_rd == 1)
			return L_R_ROTATE;
	}
 
	return UNDEFINED;
}
（5） 旋转操作，并调整旋转后节点的高度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

avl_tree_node_t* __avl_tree_rotate(avl_tree_node_t *p_node, rotate_type_t type)
{
	if(p_node == NULL)
		return NULL;
	p_node->depth -= 2;
	switch(type){
		case L_ROTATE:
			p_node = __left_rotate(p_node);
			break;
		case R_ROTATE:
			p_node = __right_rotate(p_node);
			break;
		case R_L_ROTATE:
			p_node->p_left->depth -= 1;
			p_node->p_left->p_right->depth += 1;
			p_node->p_left = __right_rotate(p_node->p_left);
			p_node = __left_rotate(p_node);
			break;
		case L_R_ROTATE:
			p_node->p_right->depth -= 1;
			p_node->p_right->p_left->depth += 1;
			p_node->p_right = __left_rotate(p_node->p_right);
			p_node = __right_rotate(p_node);
			break;
		default:
			p_node->depth += 2;
			break;
	}
 
	return p_node;
}
运行效果如下：
输入数据：
avl_tree_03
创建AVL Tree：
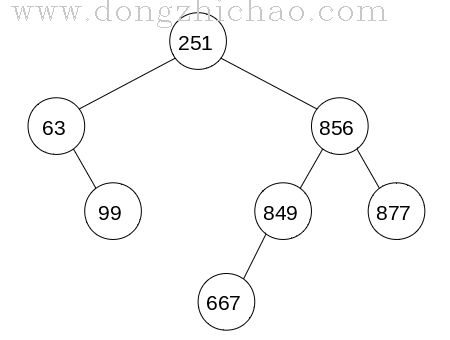
avl_tree_04
完整程序已经托管到github中，请访问：https://github.com/plumpyomi/algorithm.git

发表评论